| Macam-macam Rumus/Teori

07.16 |

1 . Rumus Kubus

Kubus merupakan bangun ruang tiga dimensi yang dibatasi enam bidang sisi berbentuk bujur sangkar. Perhatikan gambar kubus berikut ini.

Berdasarkan gambar diatas kita dapat mengetahui

jumlah sisi =6

jumlah titik sudut = 8

jumlah rusuk = 12

Rumus Luas Kubus = 6.S²

Rumus Volume Kubus = S³

Rumus Diagonal Sisi/Diagonal bidang kubus=S√2

Sehingga rumus diagonal sisi selutuhnya=12.S√2

Rumus Diagonal Ruang Kubus= S√3

Sehingga rumus diagonal ruang seluruhnya= 4.S√3

Luas Bidang Diagonal =S²√2

Sehingga Luas Bidang Diagonal Seluruhnya = 6.S²√2

2 . Rumus Balok

Balok merupakan sebuah bangun ruang tiga dimensi yang dibentuk dari tiga pasang persegi atau persegi panjang dimana satu pasang diantaranya berukuran berbeda. Bangun berbentuk balok dapat kita jumpai dalam kehidupan sehari-hari seperri lemari es, pintu, lemari pakaian, dll. Untuk lebih jelasnya perhatikan gambar balok dibawah inj.

Berdasarkan gambar diatas kita dapat mengetahui

jumlah sisi balok = 6 , dimana

sisi alas kongruen dengan sisi atas
sisi depan kongruen dengan sisi belakang
sisi kanan kongruen dengan sisi kiri

jumlah rusuk balok = 12

jumlah titik sudut balok = 8

Balok yang dibentuk oleh enam persegi yang sama dan sebangun disebut kubus.

Rumus Luas permukaan balok = 2.(p.l+l.t+p.t)

Rumus Volume balok = p.l.t

Panjang diagonal ruang balok =

Panjang diagonal sisi balok =

Sehingga luas bidang diagonal balok =

dari gambar disamping yang dimaksud dengan diagonal ruang yaitu b-h, untuk diagonal ruang yang lain dapat anda tentukan sendiri dengan melihat gambar disamping.

Yang dimaksud dengan diagonal bidang / diagonal sisi yaitu b-g. Untuk diagonal bidang yang lain dapat anda tentukan dengan melihat gambar disamping sebagai latihan.

Gambar balok disamping akan menunjukan bidang diagonal. Salah satu contoh bidang diagonal yang ditunjukan pada gambar disamping yaitu a-b-g-h. Untuk bidang diagonal yang lain dapat anda tentukan sendiri berdasarkan gambar sebagai latihan. Karena matematika itu perlu banyak latihan, bisa karena biasa.

3 . Rumus Prisma

Prisma merupakan bangun ruang tiga dimensi yang dibatasi oleh dua sisi segi banyak yang sejajar dan kongruen. Perhatikan gambar prisma segitiga dibawah ini.

Prisma segitiga diatas memiliki 5 buah sisi, 9 buah rusuk dan 6 buah titik sudut. Limas dengan alas dan tutup disebut Balok dan prisma dengan alas dan tutup berbentuk lingkaran disebut dengan tabung. Prisma memiliki ciri terdapat sisi-sisi yang saling berpotongan menurut rusuk-tusuknya yang sejajar. Berikut ini rumus luas dan volume prisma.

Rumus Luas Prisma

Luas Prisma = (2.luas alas )+ luas selubung

Sehingga luas prisma = jumlah luas sisi-sisinya

Jadi untuk menghitung luas prisma pertama kita harus menghitung luas masing-masing sisinya kemudian kita jumlahkan luas sisi-sisi prisma tersebut.

Rumus Volume Prisma

Volume Prisma =luas alas ×tinggi

Misalnya untuk prisma segitiga maka rumusnya menjadi

Volume Prisma segitiga =(½.alas segitiga.tinggi segitiga)×tinggi prisma

Sedangkan untuk prisma segiempat maka

Volume Prisma Segiempat = (panjang.lebar)×tinggi prisma.n

Begitupun untuk prisma segi-segi yang lain.

4 . Rumus Limas Segitiga Dan Segi empat

Limas merupakan salah satu bangun ruang yang tidak lepas dalam kehidupan matematika, sebelumnya telah kita bahas salah satu bangun ruang yaitu Tabung dalam artikel Rumus Menghitung Luas dan Volume Tabung Serta Aplikasinya. Dan kali ini kita akan membahas rumus-rumus dalam Limas. Berikut ini gambar bangun ruang limas

Limas Segitiga

Gambar untuk limas segitiga sebagai berikut

Limas segitiga disamping memiliki

jumlah sisi : 4

jumlah rusuk : 6

titik sudut :4

hal diatas tidak perlu dihafalkan, kita cukup melihat gambarnya maka kita dapat menghitungnya, yang penting kita tahu mana sisi, mana rusuk, dan mana titik sudut.

Rumus Luas Limas Segitiga = jumlah luas keempat sisinya

Rumus Volume limas segitiga yaitu V = 1/3 x {1/2 x Panjang x Lebar } x Tinggi

Limas Segi Empat

Berikut ini gambar limas segempat

Limas disamping memiliki :

Jumlah sisi : 5

Jumlah rusuk : 8

Jumlah titik sudut : 5

Sama halnya dengan limas segitiga, untuk limas segiempat dalam menentukan jumlah sisi, rusuk ataupun titik sudut kita tidak perlu menghafalkannya. Kita cukup melihat bagaimana gambarnya dan menghitung jumlah masing-masing.

Luas limas segi empat = luas alas + luas selubung

dimana :

luas alas = sisi×sisi

luas selubung = (½×alas×tinggi)×4

Volume limas segiempat =1/3 x Panjang x Lebar x Tinggi

5 . Rumus Tabung

Rumus Matematika akan memaparkan tentang tabung baik dari bentuk, ciri-ciri, luas dan volume yang pastinya sudah tidak asing lagi bagi kita. Sebelumnya kita lihat dulu gambar bentuk tabung berikut ini.

dimana tabung tersebut mempunyai ciri-ciri terdapat 2 rusuk, alas dan tutupnya berupa lingkaran serta mempunyai 3 bidang sisi yaitu alas, selimut dan tutup. Berikut ini rumus luas permukaan tabung yang harus kita ingat agar jika kita menemukan soal tentang luas permukaan tabung kita langsung dapat menjawabnya.

( Luas Permukaan )

r pada rumus disamping merupakan jari-jari dari alas tabung yang berupa lingkaran. Jadi rumus luas permukaan tabung sama saja dengan rumus luas lingkaran karena permukaan tabung adalah lingkaran.

Untuk selimut tabung, jika kita ingin menghitung luas selimut tabung kita dapat menggunakan rumus sebagai berikut :

Dan jika kita ingin menghitung volume atau isi tabung kita dapat menggunakan rumus sebagai berikut.

Rumus volume disamping merupakan rumus kuas alas dikali tinggi. Karena alas tabung berupa lingkaran maka rumus volume merupakan rumus luas lingkaran dikalikan tinggi tabung. Agar lebih mudah mengingatnya kita ingat saja bentuk tabung, dari situ kita akan lebih mudah mengingat baik rumus luas ataupun rumus volume tabung.

Contoh soal :

Diketahui sebuah tabung mempunyai jari-jari 14 dan mempunyai tinggi 10, berapakah luas permukaan tabung serta hitung volume dari tabung tersebut ?

jawab :

permukaan tabung merupakan sebuah lingkaran sehingga kita akan menghitung luas lingkaran.

22/7 x 14 x 14
=616

selanjutnya untuk menghitung volume tabung hasil luas permukaan diatas kita kalikan dengan tinggi tabung.

volume tabung = 616 x 10

= 6.160

jangan lupa tambahkan komentar pada kolom yang tersedia dan jika ada yang ingin ditanyakan akan saya coba jawab untuk artikel yang selanjutnya.

6 . Rumus Kerucut

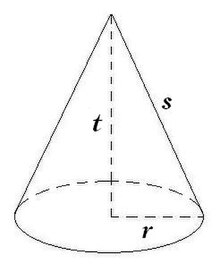
Kerucut merupakan sebuah limas istimewa yang beralaskan sebuah lingkaran dan bercirikan memiliki 2 sisi dan 1 rusuk. Sisi tegak dari kerucut bukalah segitiga tapi merupakan bidang lengkung yang disebut sebagai selimut kerucut. Pada kehidupan sehari-hari kita juga sering menemukan benda yang menyerupai kerucut misalnya menara dan nasi tumpeng. Untuk lebih jelasnya perhatikan gambar kerucut dibawah ini.

Juka gambar diatas dipisahkan antara selubung dan alas maka akan tampak seperti berikut ini.

Berdasarkan gambar maka

Rumus Alas Luas Kerucut =

Rumus Luas Selimut Kerucut =

Sehingga luas permukaan kerucut = luas alas + luas selimut

Dan volume kerucut =

dimana π = 3,14 atau 22/7

7 . Rumus Bola

Bola pastinya sudah tidak asing lagi bagi kita, sering kita jumpai dalam sehari-hari baik bola sepak, bola bekel, bola tenis, dll. Kali ini kita akan membahas rumus bola, baik dari luas atau volumenya. Secara matematika bola merupakan sebuah bangun ruang yang dibatasi oleh sisi lengkung atau disebut juga sebagai kulit bola. Sedang unsur dari bola yaitu memiliki satu sisi saja. Perhatikan gambar bola dibawah ini